*Basic

The Seven Bridges of Konigsberg is a historically notable problem in mathematics.[1] Its negative resolution by Leonhard Euler in 1736 laid the foundations of graph theiroy and preconfigured the idea of topology.[2]

**Intermediate

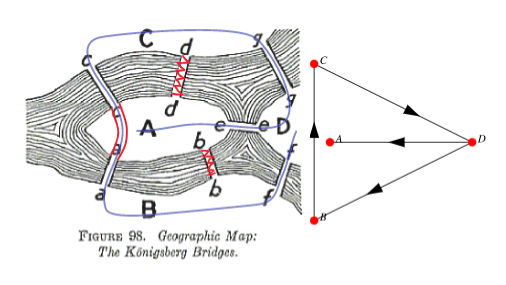
It is impossible to travel the bridges in the city of Konigsberg once and only once. Euler proved that the number of bridges must be an even number, for example, six bridges instead of seven, if you want to walk over each bridge once and travel to each part of Konigsberg.[3] So the Konigsberg bridge problem asks if the seven bridges of the city of Konigsberg can all be traversed in a single trip without doubling back, with the additonal requirement that the trip ends in the same place it began.[4] This is equivalent to asking if the multigraph on four nodes and seven edges has an Eulerian cycle. The problem was answered in the negative by Euler, and respresented the beginning of graph theory.[5]

***Advanced

J. Kahre observes that bridges b b and d d no longer exist and that a a and c c are now a single bridge passing above A with a stairway in the middle leading down to A. Even so, there is still no Eulerian cycle on the nodes A, B, C and D using the modern Konigsberg bridges, although there is an Eulerian path (right figure). An example Eulerian path is illustrated in the right figure below where, as a last step, the stairs from A to a a c c can be climbed to cover not only all bridges but all steps as well.[6]

Sources

[1] Editors. Leonard Euler's Solution to the Konigsberg Bridge Problem. Maa.org
[2] Editors. The 7 Bridges of Konigsberg. Kidscodecs.com
[3] [6] Editors. Konigsberg Bridge Problem. Mathworld.wolfram.com
[4] Editors. The Seven Bridges of Konigsberg. Mathisfun.com
[5] Editors. Konigsberg Bridge Problem. Encyclopedia Britannica. Britannica.com